Introduction
核心的观点就是训练的时候我们希望模型越大能力越强越好，因为大模型可以很轻易的从数据集中获取到想要的信息，并且我们还会用一些方法来把多个训练的模型集成在一起进行预测，这样也能够 使得预测的结果更加精确，但是在部署的时候，我们却因为计算能力的限制希望模型越小越好。因此本文提出了模型蒸馏，意思是把训练好的复杂的大模型迁移到部署的小模型上面。 核心方法就是使用训练模型的soft label来作为GT训练小模型，而不是数据集的hard label。
文章里面有个很有意思的观点，就是说soft label中被我们忽略的概率很小的那一类往往蕴含了一些generalize的信息（这也是符合信息熵的定义的）。举个例子，在MNIST 数据集上，有一种2的版本被判断为3的soft label是1e-6，被判断为7的是1e-9，这其实可以说明这种2比起7来更像3。
Method
最主要的就是提出了一种带有Temperature的新softmax表达式
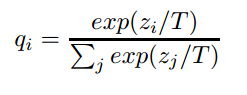T就是Temperature，这个一个可控的变量，当T=1的时候，这就是标准的softmax，T越高，得到的不同种类之间的概率分布就更加soft（原文：Using a higher value for T produces a softer
probability distribution over classes.）
实际的方法就是训练一个大模型，然后在模型的最后一层使用带有T的softmax来获得soft label，并且用这个soft label来训练小模型，需要注意的是小模型在训练的时候也是用带有同样T的softmax，训练完成之后在inference的阶段，小模型的softmax的T依然设置为1。
当训练小模型的数据集同时具有真实的GT label的时候，我们还可以把两种方法结合起来，即训练的时候既用soft label的loss来更新梯度，也用hard label的loss来更新梯度，但是这就会遇到两种loss的权重问题。作者发现，当hard label的loss权重较低时，效果比较好。原因是soft label的loss产生的梯度的幅值会变成原来的，所以我们需要在权重那里把乘回去，这样子才能保证两种loss在梯度上的贡献差不多，同时也保证了不需要随着T的变化每次都重新调参。
Thought
又看了一些相关的论文，可以理解的就是soft label利用的是不同种类之间的相似关系，并且基于此提出了了一种loss。 一点想法，使用这种soft label来训练小模型，梯度更新上真的比普通的softmax来的更好么，留个坑，手算一波有时间把结果贴上，看看T对于反向传播的影响是不是是真的是。
